Acwing算法基础课 | Samuel Hu’s Blog

type

status

date

slug

summary

1. 基础算法

1.1 排序

1.1.1 快速排序(不稳定)

快速排序是基于分治的思想

快速排序步骤

设有一个无序数组为q[n]n为数组大小

确定分界点x：q[l] ,q[r] ,q[(l+r)/2],随机选择
🌟调整区间：让所有小于等于x的数在x的左半边，所有大于等于x的数在x的右半边
递归处理左右两段

调整区间的方法

方法1(暴力):

新开两个数组a[]b[]
扫描数组q[n]：q[i] ≤ x，则将q[i]存入a数组；q[i] ≥ x，则将q[i]存入b数组
最后将两个数组a[]b[]合并到q[]

方法2(双指针挖坑法)：

给定原始数列如下，要求从小到大排序：

首先，我们选定基准元素pivot，并记住这个位置index，这个位置相当于一个“坑”。并且设置两个指针left和right，指向数列的最左和最右两个元素：

接下来，从right指针开始，把指针所指向的元素和基准元素做比较。如果比pivot大，则right指针向左移动；如果比pivot小，则把right所指向的元素填入坑中。
在当前数列中，1 < 4，所以把 1 填入基准元素所在位置，也就是坑的位置。这时候，元素 1 本来所在的位置成为了新的坑。同时，left向右移动一位。

此时，left左边绿色的区域代表着小于基准元素的区域。
接下来，我们切换到left指针进行比较。如果left指向的元素小于pivot，则left指针向右移动；如果元素大于pivot，则把left指向的元素填入坑中。
在当前数列中，7 > 4，所以把 7 填入index的位置。这时候元素 7 本来的位置成为了新的坑。同时，right向左移动一位。

此时，right右边橙色的区域代表着大于基准元素的区域。
下面按照刚才的思路继续排序：
8 > 4，元素位置不变，right左移

2 < 4，用2来填坑，left右移，切换到left。

6 > 4，用6来填坑，right左移，切换到right。

3 < 4，用3来填坑，left右移，切换到left。

5 > 4，用5来填坑，right右移。这时候left和right重合在了同一位置。

这时候，把之前的pivot元素，也就是 4 放到index的位置。此时数列左边的元素都小于 4，数列右边的元素都大于 4，这一轮交换终告结束。

快速排序模版

1.1.2 归并排序(稳定)

归并排序是基于分治的思想

归并排序步骤

设有一个无序数组为q[n]n为数组大小

确定分界点x：mid = (l+r)/2
递归排序left和right
归并(合二为一)

双指针算法

归并排序模版

1.2 二分查找算法

1.2.1 整数二分

整数二分的步骤

case 1:

找到中间值：mid = (l + r + 1) / 2
判断并更新：

case 2:

找到中间值并判断：mid = (l + r) / 2
判断并更新：

整数二分模版

1.2.2 浮点数二分

浮点数二分的步骤

找到中间值并判断：mid = (l + r) / 2
判断并更新：
满足则找到

浮点数二分模版

1.3 高精度(C++专属)

大整数存储方法：利用数组将每一位都存入数组，从头至尾为个位、十位、百位等等

1.3.1 高精度加法

高精度加法模版

1.3.2 高精度减法

高精度减法模版

1.3.3 高精度乘法

高精度乘法模版

1.3.4 高精度除法

高精度除法模版

1.4 前缀和与差分

1.4.1 一维前缀和

求和方法：利用递推s[i] = s[i - 1] + a[i]，此处规定s[0] = 0

注意：数组下标从1开始，减少特判

作用：快速求出原数组一段的和，比如求区间a[i]的和为s[r] - s[l - 1]

前缀和模版

1.4.2 二维前缀和

计算矩阵的前缀和： s[x][y] = s[x - 1][y] + s[x][y - 1] - s[x - 1][y - 1] + a[x][y]

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为： s = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]

二维前缀和模版

1.4.3 一阶差分

差分是前缀和的逆运算，对于一个数组a，其差分数组b的每一项都是a[i]和前一项a[i − 1]的差

注意：差分数组和原数组必须分开存放！！！！

作用：如果想要给a数组从[l,r]的所有数都加上c那么直接操作差分数组：B[l] += c, B[r + 1] -= c

一阶差分模版

1.4.4 二维差分数组

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：

S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

二维差分模版

1.5 双指针

常见问题分类：

对于一个序列，用两个指针维护一段区间
对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

双指针模版

1.6 位运算

求n的第k位数字: n >> k & 1

返回n的最后一位1：lowbit(n) = n & -n

位运算模版

1.7 整数保序离散化

适用条件：值域很大，但是用到的数比较少

离散化的本质是建立了一段数列到自然数之间的映射关系(value -> index)，通过建立索引引，来缩小目标区间，使得可以进行一系列连续数组可以进行的操作比如二分，前缀和等……

离散化首先需要排序去重：

排序：sort(alls.begin(),alls.end())

去重：alls.earse(unique(alls.begin(),alls.end()),alls.end());

离散化模版

例题：

1.8 区间合并

区间合并模版

思路：可以先按左端点排序，再维护一个区间，与后面一个个区间进行三种情况的比较，存储到数组里去

2. 数据结构

2.1 链表(数组模拟)

e[N]:节点的值 ne[N]:next指针

2.1.1 单链表(邻接表：存储图和树)

链表基本操作模版

2.1.2 双链表(优化某些问题)

双链表基本操作模版

2.2 栈与队列：单调队列、单调栈

2.2.1 栈

数组实现栈模版

2.2.2 单调栈

单调栈模版

https://www.acwing.com/solution/content/27437/

2.2.3 队列

数组实现队列模版

2.2.4 单调队列(滑动窗口最值)

单调队列模版

2.2.5 单调栈和单调队列解释

例子1：单调栈 —— 下一个更大元素问题

问题描述：

给定数组 [2, 1, 5, 6, 2, 3]，对于数组中每个元素，找出其右侧第一个比它大的数。如果不存在，则记为 -1。

步骤讲解：

初始化：

结果数组初始化为 [-1, -1, -1, -1, -1, -1]

空栈，用来存放元素的下标，栈内保持单调递减(从栈底到栈顶依次变小)

遍历数组：

i = 0, 元素 = 2

栈为空，直接将下标 0 入栈。
栈状态： [0] (对应元素：[2])

i = 1, 元素 = 1

栈顶下标为 0，对应元素 2，比较：1 ≤ 2
当前元素不大于栈顶元素，直接将下标 1 入栈。
栈状态： [0, 1] (对应元素：[2, 1])

i = 2, 元素 = 5

检查栈顶下标 1，对应元素 1：5 > 1，说明 5 是下一个更大元素

更新结果：result[1] = 5
弹出下标 1。

继续检查新栈顶下标 0，对应元素 2：5 > 2

更新结果：result[0] = 5
弹出下标 0。

栈空，将下标 2 入栈。
栈状态： [2] (对应元素：[5])
当前结果： [5, 5, -1, -1, -1, -1]

i = 3, 元素 = 6

检查栈顶下标 2，对应元素 5：6 > 5

更新结果：result[2] = 6
弹出下标 2。

栈空，将下标 3 入栈。
栈状态： [3] (对应元素：[6])
当前结果： [5, 5, 6, -1, -1, -1]

i = 4, 元素 = 2

检查栈顶下标 3，对应元素 6：2 ≤ 6

当前元素不大于栈顶，直接将下标 4 入栈。

栈状态： [3, 4] (对应元素：[6, 2])
当前结果保持不变

i = 5, 元素 = 3

检查栈顶下标 4，对应元素 2：3 > 2

更新结果：result[4] = 3
弹出下标 4。

继续检查新栈顶下标 3，对应元素 6：3 ≤ 6

不再满足条件，直接将下标 5 入栈。

栈状态： [3, 5] (对应元素：[6, 3])
当前结果： [5, 5, 6, -1, 3, -1]

结束处理：

遍历结束后，栈中剩余的下标(3和5)的元素右侧都没有更大的数，结果保持为 -1。

最终结果：

对于 [2, 1, 5, 6, 2, 3]，下一个更大元素依次为 [5, 5, 6, -1, 3, -1]。

例子2：单调队列 —— 滑动窗口最大值问题

问题描述：

给定数组 [2, 1, 5, 6, 2, 3] 和窗口大小 k = 3，求每个窗口内的最大值。

步骤讲解：

初始化：

使用双端队列(deque)来维护一个单调递减的队列(队首为最大值下标)。

空队列，结果列表为空。

遍历数组：

i = 0, 元素 = 2

队列为空，直接加入下标 0。
队列状态： [0] (对应元素：[2])

i = 1, 元素 = 1

检查队尾下标 0，对应元素 2：2 ≥ 1

无需弹出，直接将下标 1 加入队尾。

队列状态： [0, 1] (对应元素：[2, 1])

i = 2, 元素 = 5

先从队尾开始检查：

队尾下标 1，对应元素 1：1 < 5，弹出下标 1。
继续检查新队尾下标 0，对应元素 2：2 < 5，弹出下标 0。

队列为空后，将下标 2 加入队列。
队列状态： [2] (对应元素：[5])
此时窗口 [0,1,2] 完成，窗口最大值为：array[2] = 5
结果更新： [5]

i = 3, 元素 = 6

当前窗口应为 [1,2,3]，首先检查队首下标是否在窗口内：

队首为 2，下标 2 ≥ 3 - 3 + 1 = 1，合法。

从队尾开始检查：

队尾下标 2，对应元素 5：5 < 6，弹出下标 2。

队列为空，加入下标 3。
队列状态： [3] (对应元素：[6])
窗口 [1,2,3] 最大值为：array[3] = 6
结果更新： [5, 6]

i = 4, 元素 = 2

当前窗口为 [2,3,4]，检查队首下标：

队首为 3，下标 3 ≥ 4 - 3 + 1 = 2，合法。

从队尾开始检查：

队尾下标 3，对应元素 6：6 ≥ 2，不弹出。

将下标 4 加入队尾。
队列状态： [3, 4] (对应元素：[6, 2])
窗口 [2,3,4] 最大值为：array[3] = 6
结果更新： [5, 6, 6]

i = 5, 元素 = 3

当前窗口为 [3,4,5]，检查队首下标是否在窗口内：

队首为 3，下标 3 ≥ 5 - 3 + 1 = 3，合法。

从队尾开始检查：

队尾下标 4，对应元素 2：2 < 3，弹出下标 4。
检查新队尾下标 3，对应元素 6：6 ≥ 3，不弹出。

将下标 5 加入队尾。
队列状态： [3, 5] (对应元素：[6, 3])
窗口 [3,4,5] 最大值为：array[3] = 6
结果更新： [5, 6, 6, 6]

最终结果：

对于每个大小为 3 的窗口，最大值依次为 [5, 6, 6, 6]。

2.3 KMP匹配算法

KMP算法模版

2.4 Trie(高效存储和查找字符串)

Trie 树是一种多叉树的结构，每个节点保存一个字符，一条路径表示一个字符串。

Trie模版

2.5 并查集

1.将两个集合合并 2.询问两个元素是否在一个集合中基本原理：每个集合用一棵树来表示，树根编号就是整个集合的编号，每个节点存储它的父节点，p[x]表示x的父节点

并查集模版

2.6 堆

堆是一个完全二叉树小根堆指的是根结点最小；大根堆指的是根结点最大

数组实现堆及其操作模版

2.7 哈希表

存储结构：1.开放寻址法 2.拉链法字符串哈希方式

哈希表模版

字符串哈希模版

2.8 STL简介

3. 搜索与图论

3.1 深度优先搜索(DFS)

使用数据结构是栈(Stack)，不具备最短路性质

深度优先搜索模版

3.2 广度优先搜索(BFS)

使用的数据结构是队列(Queue)，在这里有”最短路”的概念

广度优先搜索模版

3.3 树与图的存储

1.邻接表法(常用) 2.邻接矩阵法

存储模版

3.4 树与图的深度优先遍历

树和图的深度优先遍历模版

3.5 树与图的广度优先遍历

树和图的广度优先遍历模版

3.6 拓扑排序

拓扑排序模版

接下来是求最短路径问题，具体见图 迪杰斯特拉是用最短的边去更新其他边，而spfa是上次更新的终点去更新其他边，贝尔曼则是非常暴力的每次更新所有边

3.7 最短路径问题

3.7.1 Dijkstra算法

朴素Dijkstra算法：适用于稠密图堆优化Dijkstra算法：适用于稀疏图

朴素Dijkstra模版

堆优化版本的Dijkstra算法

3.7.2 bellman-ford算法（有负环用）

什么是bellman - ford算法？ Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。 (通俗的来讲就是：假设 1 号点到 n 号点是可达的，每一个点同时向指向的方向出发，更新相邻的点的最短距离，通过循环 n-1 次操作，若图中不存在负环，则 1 号点一定会到达 n 号点，若图中存在负环，则在 n-1 次松弛后一定还会更新) bellman - ford算法的具体步骤 for n次 for 所有边 a,b,w (松弛操作) dist[b] = min(dist[b],back[a] + w) 注意：back[] 数组是上一次迭代后 dist[] 数组的备份，由于是每个点同时向外出发，因此需要对 dist[] 数组进行备份，若不进行备份会因此发生串联效应，影响到下一个点在下面代码中，是否能到达n号点的判断中需要进行if(dist[n] > INF/2)判断，而并非是if(dist[n] == INF)判断，原因是INF是一个确定的值，并非真正的无穷大，会随着其他数值而受到影响，dist[n]大于某个与INF相同数量级的数即可 bellman - ford算法擅长解决有边数限制的最短路问题 时间复杂度

bellman-ford算法模版

3.7.3 SPFA算法

松弛的概念
考虑节点u以及它的邻居v，从起点跑到v有好多跑法，有的跑法经过u，有的不经过。经过u的跑法的距离就是distu+u到v的距离。所谓松弛操作，就是看一看distv和distu+u到v的距离哪个大一点。如果前者大一点，就说明当前的不是最短路，就要赋值为后者，这就叫做松弛。
spfa算法文字说明：
建立一个队列，初始时队列里只有起始点。
再建立一个数组记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。
再建立一个数组，标记点是否在队列中。
队头不断出队，计算始点起点经过队头到其他点的距离是否变短，如果变短且被点不在队列中，则把该点加入到队尾。
重复执行直到队列为空。
在保存最短路径的数组中，就得到了最短路径。

SPFA图解：
给定一个有向图，如下，求A~E的最短路。
源点A首先入队，然后A出队，计算出到BC的距离会变短，更新距离数组，BC没在队列中，BC入队
B出队，计算出到D的距离变短，更新距离数组，D没在队列中，D入队。然后C出队，无点可更新。
D出队，计算出到E的距离变短，更新距离数组，E没在队列中，E入队。
E出队，此时队列为空，源点到所有点的最短路已被找到，A->E的最短路即为8

SPFA算法模版

SPFA算法检测负环代码模版

3.7.4 Floyd算法

基于动态规划思想

Floyd算法模版

3.8 最小生成树

3.8.1 Prim算法(稠密图)

朴素版Prim算法模版

AcWing 858. Prim算法求最小生成树：图解+详细代码注释（带上了保存路径） - AcWing

AcWing,题解,Prim算法求最小生成树：图解+详细代码注释（带上了保存路径）,

https://www.acwing.com/solution/content/38312/

3.8.2 Kruskal算法(稀疏图)

Kruskal算法模版

3.9 二分图

3.9.1 染色法判断二分图

二分图当且仅当图中不含奇数环(该点出发回到该点经过的边数为奇数) 1. 什么叫二分图 有两顶点集且图中每条边的的两个顶点分别位于两个顶点集中，每个顶点集中没有边直接相连接 说人话的定义：图中点通过移动能分成左右两部分，左侧的点只和右侧的点相连，右侧的点只和左侧的点相连。 下面的图就是一个二分图：
如何判断一个图是不是二分图？
开始对任意一未染色的顶点染色。
判断其相邻的顶点中，若未染色则将其染上和相邻顶点不同的颜色。
若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图，若颜色不同则继续判断。
bfs和dfs可以搞定！

染色法判断二分图模版

3.9.2 匈牙利算法

要了解匈牙利算法必须先理解下面的概念：

匹配：在图论中，一个「匹配」是一个边的集合，其中任意两条边都没有公共顶点。
最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。

下面是一些补充概念：

完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。
交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。

该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

匈牙利算法模版

4. 动态规划

4.1 背包问题

状态其实就是代指未知数

4.1.1 0-1背包问题

每件物品最多用一次

AcWing 2. 01背包问题（状态转移方程讲解） - AcWing

AcWing,题解,01背包问题（状态转移方程讲解）,

https://www.acwing.com/solution/content/1374/

4.1.2 完全背包问题

每件物品有无限个

AcWing 3. 完全背包问题-小白专享受 - AcWing

AcWing,题解,完全背包问题-小白专享受,

https://www.acwing.com/solution/content/180720/

4.1.3 多重背包问题

每个物品最多有个，每个物品数量不一样

AcWing 5. 多重背包问题 II - AcWing

AcWing,题解,多重背包问题 II,

https://www.acwing.com/solution/content/5527/

4.1.4 分组背包问题

物品有组，每个组里只能选一个物品，每个组里的物品是互斥的

AcWing 9. 分组背包问题 - AcWing

AcWing,题解,分组背包问题,

https://www.acwing.com/solution/content/3483/

5. 贪心算法

贪心算法是一种在每一步都做出局部最优选择，从而期望能得到全局最优解的算法设计思想。它简单直观、实现高效，但并不是对所有问题都适用。

5.1 贪心算法的基本概念

5.1.1 定义与思想

贪心算法（Greedy Algorithm）在求解问题时，总是选择在当前看来最优的那一个解，即“眼前看最好的选择”。贪心算法的核心思想是：

局部最优： 每一步都选择当前状态下最优的选项，不考虑未来可能带来的影响。

全局最优： 对于满足特定条件的问题，这种局部最优的选择可以累积得到全局最优解。

5.1.2 适用条件

贪心算法并不适合所有问题，其能得到最优解的前提是问题具备以下两个性质：

贪心选择性质（Greedy Choice Property）： 通过局部最优的选择，不会破坏全局最优解的构建，即局部最优解可以构成全局最优解的一部分。

最优子结构（Optimal Substructure）： 问题的最优解可以通过其子问题的最优解来构造，即问题可以被分解为互不相干的子问题，并且其最优解包含子问题的最优解。

5.2 贪心算法的设计步骤

在设计贪心算法时，可以按照以下步骤进行考虑和实现：

问题建模： 明确问题的输入、输出以及需要达到的最优目标。

证明贪心选择性质： 分析问题，证明每次局部选择不会影响全局最优性。如果没有这一步，贪心算法可能只得到一个次优解。

建立排序或优先级结构： 贪心算法常常需要先将数据按照某种关键指标排序（例如活动选择问题中按结束时间排序），或者使用优先队列来动态选择最佳候选。

设计循环结构： 遍历数据，根据贪心策略判断是否选择某个元素，并更新状态。

返回结果： 将构造的解返回，同时分析时间复杂度与空间复杂度。

5.3 C++ 贪心算法代码模板

以下是一个较为通用的贪心算法代码模板，展示了如何对输入数据进行排序，以及如何通过循环逐步构造最终解的过程：

代码说明：

数据结构定义：

Item 结构体可以代表活动、任务或其他需要按照某种指标进行选择的对象。

排序策略：

使用 sort 函数对活动按照结束时间进行排序，以便能够优先选择最早结束的活动，从而为后续活动留出更多空间。

贪心选择条件：

在循环中，通过检查当前活动的起始时间是否不早于上一个选中活动的结束时间来判断是否可以选择该活动。

输出阶段：

输出选中的活动数量以及各活动的时间区间，验证算法的正确性。

5.4 应用实例和扩展

5.4.1 活动选择问题

上述代码模板实际上就是经典的活动选择（Activity Selection）问题的解决方案。贪心策略在这里是显而易见的：每次选择结束最早且与已选活动不冲突的活动，从而使得剩余时间最大化以便安排更多活动。

5.4.2 其他典型问题

贪心算法还适用于如下问题：

最小生成树问题： 如 Prim 算法和 Kruskal 算法。

单源最短路径问题： 如 Dijkstra 算法（带权图、非负边权）。

哈夫曼编码： 用于数据压缩。

区间调度问题、背包问题的近似算法等。

在这些问题中，设计合适的贪心策略以及证明其正确性是关键。

6. 数学知识

6.1 数论

6.1.1 质数

质数的定义：大于1的整数中，如果只包含1和它本身这两个约数，就被称为质数或素数 质数的判定：试除法

质数判断模版

分解质因数模版

筛质数模版

6.1.2 约数

求一个数约数模版

约数个数模版

理论介绍：
质因子分解：一个整数可以分解成多个质因子的乘积，假设：
其中，是的不同质因子，是这些质因子的对应指数。
约数个数公式：根据质因子分解的公式，如果，那么的约数个数为：
其中是每个质因子的指数加一，表示该质因子可能的不同取法（从到的幂次）。

约数之和模版

理论介绍
这段代码的目的是通过 质因子分解 和 公式求解 来计算一个整数集合中所有数的某种特定结果。具体来说，代码的目标是计算如下形式的结果：
对于给定的个整数，首先对每个整数进行质因子分解，求出每个质因子的幂次。然后根据以下公式计算结果：
其中，是所有质因子，是这些质因子的幂次。然后我们根据这些计算公式，在所有质因子上相乘，最终得到一个结果。

最大公约数(欧几里得算法|辗转相除法)

基本概念 最大公约数（Greatest Common Divisor，简称GCD）是指两个或多个整数共有约数中最大的一个。也称最大公因数、最大公因子。
例如，和的最大公约数记为，同样，, , 的最大公约数记为，多个整数的最大公约数也有同样的记号。
其中都是自然数。也就是说，两个数的最大公约数，将其中一个数加到另一个数上，得到的新数，其公约数不变。例如：

证明
要证明这个原理很容易：如果是和的公约数，整除，也能整除，那么就必定要整除，所以也是和的公约数，从而证明它们的最大公约数也是相等的。

辗转相除法

每一步都会缩小数字，直到其中一个数为 0，另一个数就是最大公约数。

辗转相除法模版

优化版辗转相除法

对于 (a, b)，如果，则就是最大公约数，可以提前结束循环。

欧几里得算法模版

6.2 欧拉函数

欧拉函数，也称为欧拉函数，是数论中的一个重要概念，记作。它的定义是：对于给定正整数，表示小于或等于且与互质的正整数的个数。下面将详细介绍欧拉函数的定义、基本性质，以及其推导过程。
1. 定义
对于任意正整数，欧拉函数 定义为：
区间内与互质的正整数个数。
例如， = 9 时，小于 9 的正整数为 1, 2, 3, 4, 5, 6, 7, 8，其中与 9 互质的数为 1, 2, 4, 5, 7, 8，因此 = 6。
2. 基本性质
欧拉函数具有以下重要性质：
(1) 乘法性
如果 m 与 n 互质（即 gcd(m, n) = 1），则：
这一性质说明是 乘法函数。利用这一性质，可以将任何整数分解为质因数的积后，对每个质因数的贡献分别计算。
(2) 素数幂的情形
对于素数和正整数，有：
原因在于，1 到中恰有个数能被整除，因此不能与互质。
(3) 分解公式
设的质因数分解为
则由乘法性和素数幂性质得到：
3. 推导过程
下面介绍两种常见的推导方法：利用乘法性和利用容斥原理。
3.1 利用乘法性推导
求解素数幂的情况：
如前所述，对于（其中是素数），1 到中有个数是的倍数，即不能与互质，因此：
利用乘法性：
由于欧拉函数是乘法函数（当因子互质时），对任意整数 n，其质因数分解为：
就有：
将每一项代入上面素数幂的结果，得：
因此，可以写成通式：
3.2 利用容斥原理推导
另一种常用的方法是利用容斥原理，按照以下步骤进行推导：
初始总数： 从 1 到总共个数。
去除非互质的数： 若的质因数为那么被某个质因数整除的数有大约个。直接减去这些数的个数，但注意重复计算问题。
处理重叠：
对两个不同的质因数和，被它们共同整除的数个数大约为，在第一步中被重复减去，需要加回来。
对三个质因数同时整除的数，需要再减去，……以此类推。
公式表示： 根据容斥原理，最终互质的数个数可写作：
这实际上等于：
这一形式正是之前乘法性推导中得出的结果。
4. 应用实例
以 n = 12 为例：
12 的质因数分解为；
根据公式：
实际上，1 到 12 中与 12 互质的数为 1, 5, 7, 11，共 4 个，验证了公式的正确性。
5. 结论
欧拉函数为数论中的一个基础工具，不仅具有优美的数学结构，其乘法性和容斥原理的推导方法也为解析其他数论问题提供了有力工具。通过分解质因数、应用乘法性以及容斥原理，我们可以清楚地导出：
6. 欧拉函数应用
欧拉定理：若a与n互质，那么有
费马定理：若a与p互质，p是质数，那么有

欧拉函数模版

质数筛法求欧拉函数

6.3 快速幂

可以快速的求出的值，时间复杂度是，其中a、k、p的范围都是

核心思路：反复平方法

预处理出：一共个数

当求时利用预处理的这些值组合出，即将拆成

得到，其实，就只需要把转化为二进制即可

预处理一共计算出个数，需要计算次，将拆成二进制表示，并计算结果，需要次，所以总共的时间复杂度就是。其实编写代码时，可以将上面两步合在一起，实际只需要次运算，例如

快速幂代码模板

6.4 扩展欧几里得算法

裴蜀定理：对于任意正整数，那么一定存在非零整数，使得

证明：令，则一定是的倍数，也一定是的倍数，那么也一定是的倍数，那么可以凑出最小的倍数就是1倍，即

给定如何求解就是扩展欧几里得算法

代码模板

扩展欧几里得算法用来解决这样一个问题，，求，如果是的倍数，则有解，解就是倍数乘以，否则就是无解

此外，还可以解线性同余方程/方程组，例如解，做一下变换就是，即，就可以用扩展欧几里得算法解决，878. 线性同余方程

下面给出利用扩展欧几里得算法来求解形如

的同余方程组的完整推导过程，其核心思想是利用两两合并的方法，把两个同余合并成一个，再逐步归约到一个同余形式。

1. 两两合并的基本思想

以前两个方程为例

可写成

将两式相等，即得到

我们把上式看作关于未知整数和的线性不定方程。

2. 存在解的必要条件

设

那么线性不定方程

有整数解的充要条件是

即必须是的最大公约数的倍数。

3. 利用扩展欧几里得算法求通解

假设满足上述可解条件，我们可以利用扩展欧几里得算法来求下面的等式的一个特解：

通过扩展欧几里得算法，设得到一组特解 (x{0},y{0})，则有：

接下来，将原式

写成

因为是的倍数，我们令

（其中为整数），此时原方程可写为

利用前面求出的特解，我们可以得到一个特解为

线性方程的通解形式则是（注意此处参数 k 为任意整数）：

4. 得到合并后的同余式

原来我们有

将的通解代入

由于

令

则我们得到一个等价的同余式

这就完成了将两个同余方程合并成一个的过程。

5. 逐步归约求解完整方程组

对于原方程组：

我们可以先将前两个同余合并得到新的同余

其中

接下来，再将这个结果与第三个同余

利用同样的方法合并，得到

其中

依此类推，经过反复合并后，最终将原来的 n 个方程合并成一个形如

的同余式，其中

且是在各次合并过程中计算得到的一个固定解。

6. 总结

两两合并： 对于任意两个同余

写出并得到线性方程

存在性条件： 必须要求能整除。

利用扩展欧几里得算法： 求得关于的通解，其中

,这里 )）

合并表达： 代回得到

逐步归约： 把合并后的同余与下一个同余继续合并，直到所有同余合并为一个。

6.5 中国剩余定理

有个两两互质的数，给定线性同余方程组，求

解法：令，

，用表示模的逆（）

则

中国剩余定理模版

6.6 高斯消元

高斯消元能在的时间复杂度内求解个方程，个未知数的多元线性方程组，即

对增广矩阵做初等行列变换，变成一个上三角矩阵

对某一行（列）乘以一个非零的数
交换两行（列）
将一行（列）的若干倍加到另一行（列）

解的情况有三种

无解，系数矩阵秩不等于增广矩阵的秩
有无穷多解，系数矩阵秩等于增广矩阵的秩，小于n
有唯一解，系数矩阵秩等于增广矩阵的秩，等于n

步骤

枚举每一列c
找到该列绝对值最大的一行
将这一行换到最上面
将该行第一个数变成1
将下面所有行的当前列消成0
固定该行

高斯消元法模版

6.7 求组合数

从个元素中选择个，有多少种取法

求解方法

递推式，其实是dp，数据范围组询问，，

证明，从个元素中分出一个元素，如果要选的个元素包含这个元素，那么就是从剩下的个元素中选个，即，如果不包含这个元素，就是从个元素中选择个，即，综合两种情况就是

代码模板：

预处理逆元，数据范围组询问，，预处理范围内所有数的阶乘%MOD的值和阶乘的逆元%MOD的值，然后带入，求解，

代码模板

卢卡斯定理

询问很少，但是数据范围特别大, 则

把a和b转换为p进制表示

生成函数(

所以有

对比等式

若p是质数，则对于任意整数，有：

分解质因数法求组合数

当我们需要求出组合数的真实值，而非对某个数的余数时，分解质因数的方式比较好用：

筛法求出范围内的所有质数
通过这个公式求出每个质因子的次数。中的次数是
用高精度乘法将所有质因子相乘

卡特兰数

6.8 容斥原理

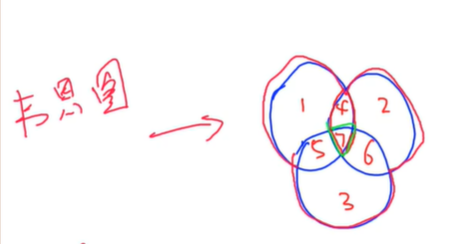
，从个数中选任意多个数的方案数

证明，

假设，存在于个集合之中，，那么被计算的次数为，

AcWing 890. 能被整除的数

6.9 博弈论

6.9.1 公平组合游戏ICG

若一个游戏满足：由两名玩家交替行动；

在游戏进程的任意时刻；

可以执行的合法行动与轮到哪名玩家无关；

不能行动的玩家判负；

则称该游戏为一个公平组合游戏。 NIM博弈属于公平组合游戏，但城建的棋类游戏，比如围棋，就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不满足条件2和条件3。

6.9.2 Nim游戏

给定N堆物品，第i堆物品有Ai个。两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取。取走最后一件物品者获胜。两人都采取最优策略，问先手是否必胜。

我们把这种游戏称为NIM博弈。把游戏过程中面临的状态称为局面。整局游戏第一个行动的称为先手，第二个行动的称为后手。若在某一局面下无论采取何种行动，都会输掉游戏，则称该局面必败。所谓采取最优策略是指，若在某一局面下存在某种行动，使得行动后对面面临必败局面，则优先采取该行动。同时，这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况，即两人均无失误，都采取最优策略行动时游戏的结果。 NIM博弈不存在平局，只有先手必胜和先手必败两种情况。 定理： NIM博弈先手必胜，当且仅当 A1 ^ A2 ^ … ^ An != 0

6.9.3 有向图游戏

给定一个有向无环图，图中有一个唯一的起点，在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿有向边进行移动，每次可以移动一步，无法移动者判负。该游戏被称为有向图游戏。任何一个公平组合游戏都可以转化为有向图游戏。具体方法是，把每个局面看成图中的一个节点，并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。

6.9.4 Mex运算

设S表示一个非负整数集合。定义mex(S)为求出不属于集合S的最小非负整数的运算，即： mex(S) = min{x}, x属于自然数，且x不属于S

6.9.5 SG函数

在有向图游戏中，对于每个节点，设从出发共有条有向边，分别到达节点，定义SG(x)为x的后继节点的SG函数值构成的集合再执行mex(S)运算的结果，即： SG(x) = mex({SG(y1), SG(y2), …, SG(yk)}) 特别地，整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值，即SG(G) = SG(s)。

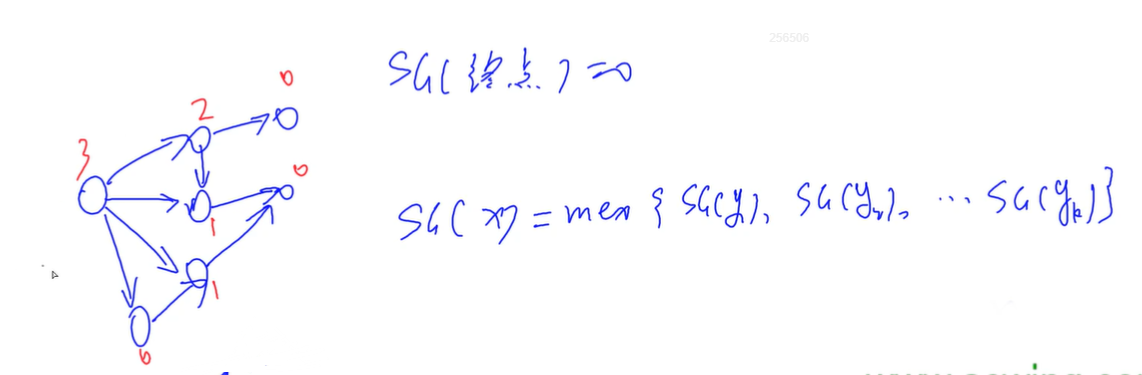
6.9.6 有向图游戏的和

设是个有向图游戏。定义有向图游戏，它的行动规则是任选某个有向图游戏，并在上行动一步。被称为有向图游戏的和。有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数值的异或和，即： SG(G) = SG(G1) ^ SG(G2) ^ … ^ SG(Gm)

定理 有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。